在行測數量關系的考查中,總會有一些難題,讓考生們望而生畏,有些題目如果用常規方法來求解,不僅過程復雜難度大,而且耗時長,讓考生們不得不放棄它們,然而事實上只要掌握正確方法,通常是可以簡化計算,快速得出答案的。比如古典概率,今天MVP學習網就帶大家一起來學習一下古典概率中的定位法。
【應用環境】古典概率題目中對兩個元素的相對位置有要求(同一排、同一趟車、同一組、不同組……)。
【方法簡述】解題時,可以先確定一個元素的位置,再考慮另一個元素的位置可能的樣本數(分母)和位置滿足題目要求的樣本數(分子)。
【例1】一張紙上畫了5排共30個格子,每排格子數相同,小王將1個紅色和1個綠色棋子隨機放入任意一個格子(2個棋子不在同一格子),則2個棋子在同一排的概率:
A.不高于15% B.高于15%但低于20%
C.正好為20% D.高于20%

以上的求解過程是我們按照常規的思路和解題方法來進行的,下面我們再來看一下如何利用定位法求解這道題。
方法二,題目要求2個棋子在同一排,這體現對于兩個元素的相對位置有要求,那么我們就可以先固定其中一個棋子,再去考慮另一個棋子的情況。具體來說,可以先從30個格子中任選1個格子安排紅色棋子,那么在安排綠色棋子時,一共還剩下29個空格子,若想2個棋子在同一排,則綠色棋子只能挑選紅色棋子所在那一排中剩余的5個格子里的1個,故2個棋子在同一排的概率為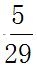 ×100%≈17%,選擇B項。
×100%≈17%,選擇B項。
通過例1的講解,我們不難發現,一道解題過程比較復雜的古典概率題目通過定位法,可以化繁為簡,快速求解,那么接下來讓我們再練習一道更有挑戰性的題目鞏固一下技巧。
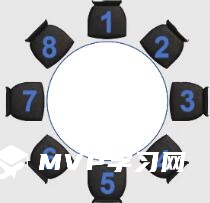
【例2】某次圓桌會議共設8個座位,有4個部門參加,每個部門2人,排座位時,要求同一部門的兩人相鄰,若小李和小王代表不同部門參加會議,則他們座位相鄰的概率是:

【答案】D。核心解析:這道題目若采用常規方法求解十分復雜,這里并不過多贅述,題目要求小李和小王座位相鄰,這體現了對于兩個元素的相對位置是有要求的,所以我們通過定位法快速求解,我們先將其中一人固定,再考慮另一人情況。如下圖所示,讓小李先隨機選定1個座位(比如1號座位),根據題干,求同一部門的兩人需相鄰,則小李選完座位之后,小李的部門同事只能坐在其旁邊的座位上(2號或8號座位),那么在安排小王的座位時,除去被占的2個座位一共還剩下6個座位,其中只有1個座位能滿足與小李相鄰,故小李和小王座位相鄰的概率為1/6,選擇D項。
以上就是關于定位法的講解和應用,MVP學習網希望大家能夠認真學習,多加練習,熟練掌握技巧,這樣大家就都可以將這一類的古典概率題目一招“定”乾坤。

